|
|
|
|
|
|
Motivation
Our dexterous telemanipulation system uses
the CyberGlove®, from Immersion
Corp., as an input device. When performing dexterous telemanipulation, it
is imperative to calibrate the CyberGlove® to each individual user to ensure
repeatable and accurate results. Therefore, we need to devise a scheme to calibrate
the user-glove system in a way which is suitable for our telemanipulation task.
For our current set-up, we use only the index finger and thumb, to mimic the
pinching grasp which the robot
is capable of.
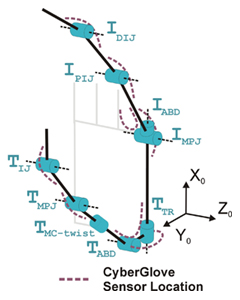
Parameter Identification
Three issues are central to calibration
of a user wearing the CyberGlove®: the fit of the glove, the properties
of the sensors, and the kinematic model of the human hand used to extrapolate
the finger positions. The dataglove measures finger joint angles using a proprietary
analog bend sensor. Therefore we need to know the conversion factor ("gain")
from the analog sensor values to radian angle measurements, as well as a constant
offset term. This results in two parameters for each sensor, according to the
equation:
angle (radians) = gain * (analog sensor reading) + offset
In addition, the human thumb has complex
kinematics which are not accurately measured by the CyberGlove® in its default
configuration. The thumb base joint (trapeziometacarpal joint or TMJ) is a 2-degree-of-freedom
rotational joint: its two axes of rotation are neither intersecting nor perpendicular.
The two sensors on the CyberGlove® associated with that joint do indeed
measure two degrees of freedom, but these rotational axes too are neither perpendicular
nor intersecting. Rather than develop a complicated relationship between the
sensors and the actual kinematics of the thumb, we chose to assume that the
two TMJ angles were each linear functions of the two sensors:
TMJ angle (radians) = gain1 * (sensor 1) + gain2 * (sensor
2) + offset
 We
can extend this cross-coupling to include other joint-sensor relationships as
well. The second thumb joint (metacarpophalangeal joint MPJ) actually has two
degrees of freedom: in addition to the obvious flexion, it twists and yaws as
well (they are inter-related). These additional degrees of freedom are not easily
controllable by the human, but are mostly responsive to forces exerted on the
thumb. We
can extend this cross-coupling to include other joint-sensor relationships as
well. The second thumb joint (metacarpophalangeal joint MPJ) actually has two
degrees of freedom: in addition to the obvious flexion, it twists and yaws as
well (they are inter-related). These additional degrees of freedom are not easily
controllable by the human, but are mostly responsive to forces exerted on the
thumb.
Our model assumes Hookean pin joints at
each bone intersection: the bone lengths themselves are constant. These bone
lengths are additional parameters to be calibrated. Finally, although most rotational
axes in the fingers are nearly parallel, the thumb MPJ axis is skew to the two
axes of the TMJ joint, by some unknown angle. Due to the twisting motion of
the MPJ, this 'metacarpal twist', or MCtwist, as we call it, may be a function
of some of the other thumb angles. We can employ the cross-coupled gain idea
to the MCtwist parameter as well.
In summary, we are now calibrating for
the following 30 parameters:
- One offset for each sensor (there are 8)
- One gain for each sensor (again, 8)
- Several cross-gains for cross-coupled sensors, including the
effect of sensors on the MCtwist (we used at least 5 of these)
- the length of each bone (there are 8 of these as well)
- the base MCtwist offset angle (only 1 of these)
Calibration Theory
Rohling and Hollerbach, in an earlier paper,
describe a method of calibrating a kinematic model of a human hand, concerned
with the offset angles only (i.e. no bone lengths or gains). We extend that
model to include sensor gains, bone lengths, and cross-coupling factors.
Without going into the
gory details, the calibration method proceeds as follows: several 'poses'
of the hand are captured, while the user is wearing the glove. The exact positions
of the finger tips are recorded, as well as the uncalibrated joint angles. Using
knowledge of the kinematics of the hand, we can come up with an iterative solution
which minimizes the error between a calculated fingertip position and the actual,
measured fingertip position. After several iterations, and provided that the
set of 'poses' is sufficiently large, we can obtain actual values for the unknown
parameters which allow us to accurately extrapolate the 3-dimensional position
of the user's fingertips, given only the sensor readings from the CyberGlove®.
Calibration Implementation
Rather than use an external measurement
device (such as a stereoscopic vision system) to capture the actual positions
of the user's fingertips, we used a different, rather sneaky approach. If we
instruct the user to touch his or her fingertips together while gathering the
poses, we can approximate a closed kinematic chain. With the fingertips held
together, and the fingers moving around, we can gather approximately 20 seconds
of data, and calibrate from this data. Granted, it's not entirely accurate:
we assume that the fingertips are in exactly the same position, when
in reality they move relative to each other, due to rolling contact and soft
tissue deformation. It is, however, sufficiently accurate to provide us with
accuracy on the order of ±4mm. Compare this to the uncalibrated accuracy,
which is in general worse than ± 30mm, which is quite unacceptable for
fine telemanipulation tasks. From our experiments, we have determined that this
calibration accuracy is sufficient for the tasks which we wish to perform.
The calibration results are demonstrated
in this MOVIE!!. Watch the
correspondence between the user's fingers and the computer model, both before
and after calibration.
Additional Material
The calibration method is covered in the
following publication:
W.B. Griffin, R.P. Findley, M.L. Turner, and M.R. Cutkosky, "Calibration
and Mapping of a Human Hand for Dexterous Telemanipulation", Presented
at ASME IMECE 2000 Symposium
on Haptic Interfaces for Virtual Environments and Teleoperator Systems
More indepth coverage can be found in Michael Turner's PhD Thesis in Chapter
4 and Appendix A and B:
Michael L. Turner, Programming
Dexterous Manipulation by Demonstration, 2001 (.pdf 1.4 MB) |
|

