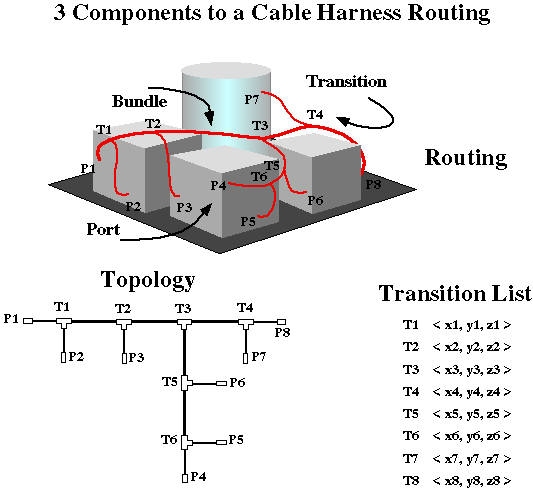


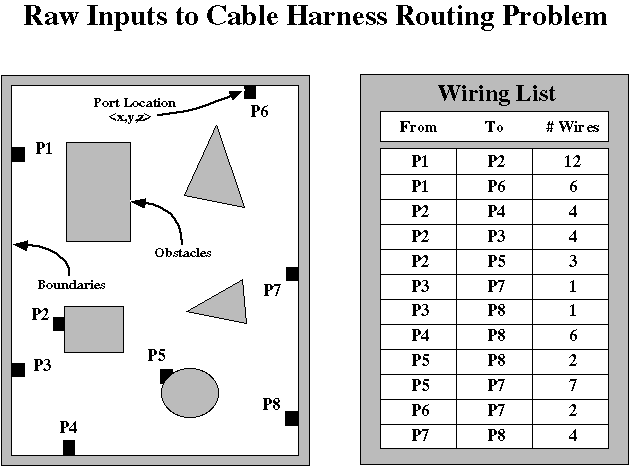
The raw inputs to CHRP are an environment which defines the port locations, boundaries, and obstacles as well as a wiring list that specifies how many wires are to routed between ports.
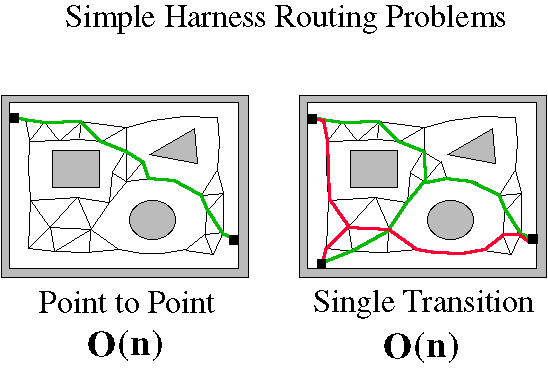
The routing problem is more difficult than point-to-point routing in that the transition, or breakaway, locations are not known until after the harness is routed. The figure below shows that when more than two locations are to be connected, the paths are dependant of where the transistion is located.
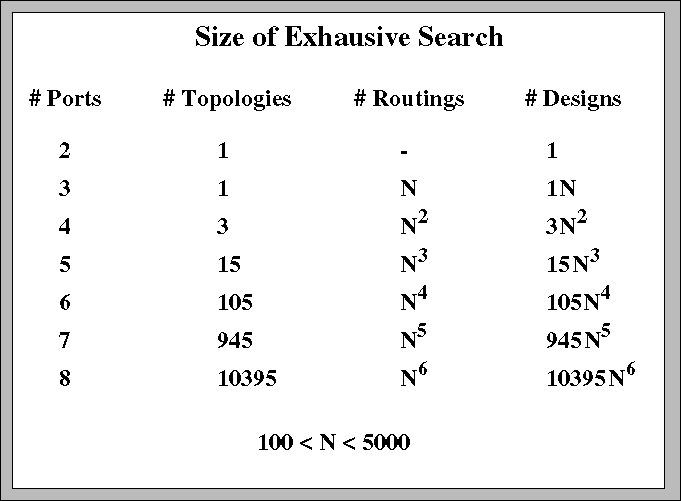
The number of routing combinations increase factorially with the number of ports. As a example, consider the following graph with 4 ports. Not only are there several possible routings but several distinct topologies.

The following table shows how the search space increases dramatically with the number of ports
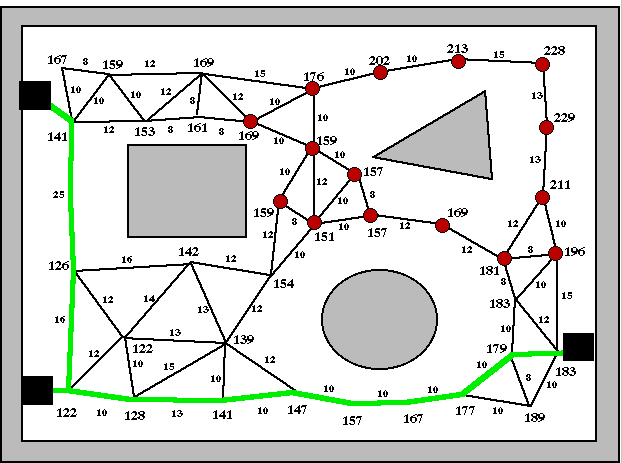
Two characteristics of the search problem makes solving this problem using tradition gradient-based search methods ineffective. The first is that the search space is highly convex. The following figure shows a simple 3-port harness with the cost assocated to moving the single transition to each graph location labled on the graph nodes. All the nodes with a red dot are ones in which a gradient search method would result in a local minima.
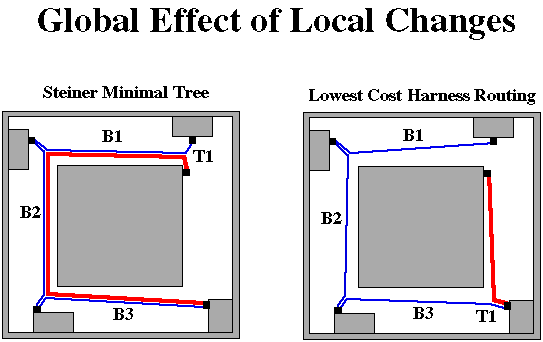
The second challenge is that a small local change in topology results in large global change as shown below.