GA Introduction to the CHRP
Product design is typically a process of educated trials and errors in which one or more designs are modified, enhanced, or scrap in the quest to find a better design. It is not uncommon to hear designers refer to their work as an evolutionary process. Evolutionary processes share some common features such as an ability to combine and modify inputs to produce new, hopefully better, outputs. As teams of designers become more commonplace in modern design, this evolutionary process becomes one of agents sharing knowledge encapsulated in design fragments. Likewise in the computational design arena, software agents should work together.
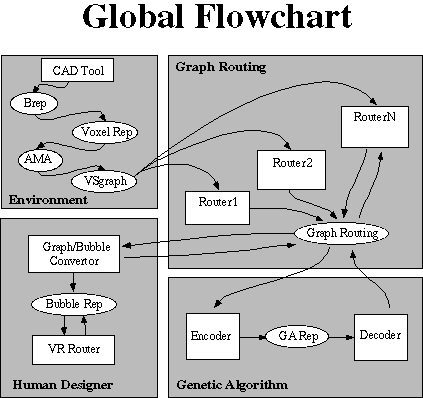
The goals of the agent architecture are to allow a number design tools to share their findings with one another and to allocate resources commensurate to each tool’s performance. Collaboration is facilitated by the use of a shared work repository, similar to a blackboard, into which complete designs are stored. The collection of designs at a given time is called a population of designs. Now, as in genetic approaches, this population of designs will be used as input to a number of tools to create a new, hopefully better, population. These heuristic, evolutionary, or human-based tools called operators in GA and agents in this paper, fall into three main categories: creators, mutators, or combinors.
1. Creators:
Creators do not require any inputs other than the problem specifications to generate a complete design. Typically they are used at the beginning of the design process to “seed” the initial design population. They can also be used as the design evolves to add new ideas to stale designs.
2. Mutators:
Mutators take a single design and alters only a small subset of the design parameters. Typically, the original design is lost after a mutation. Simple gradient search or simulated annealing procedures could be classified as mutators. In general, Mutators with domain knowledge outperform s those without. Mutator use domain knowledge to retain useful design fragments while modifying fragments of lower quality. Mutators are often used to improve designs that have some poor components as well as to introduce additional ideas.
3. Combinors:
Combinors take two or more designs as inputs and attempt to extract positive fragments from each of them to produce a new design. In order for a Combinor to be successful, it must be able to determine what fragments have high value as well as understand the relationships between design fragments of different designs to find compatible matches. Combinors, therefore, require far more domain knowledge than Mutators.
These agents can communicate indirectly by reading each other's designs from the previous population and writing the new ones into the next population. The figure below illustrates the flowchart of the design process.
Routing at two levels
The CHRP can be thought as a problem of two levels. At the higher level, a harness can be viewed simply as its configuration. Different configurations result in different numbers of wires in each of transbundles, and different bundle lengths as it's routed onto the AMA graph. At a lower level, the problem is to find this routing. Here, the topology of the harness and its port locations are defined and all that remains is to determine locations for the transitions. The figure below shows the design process separated into "configuration design" and "transition location".

Since each of the design agents discussed in this work is able to output a configuration but not all the transition locations, the configuration is used as the lowest common denominator between the agents. This separation enables both design sharing as well as focuses each design agent on a meta goal. The "transition location" process then becomes just an evaluation algorithm that takes a configuration as input and output the transition locations.
Transition Location
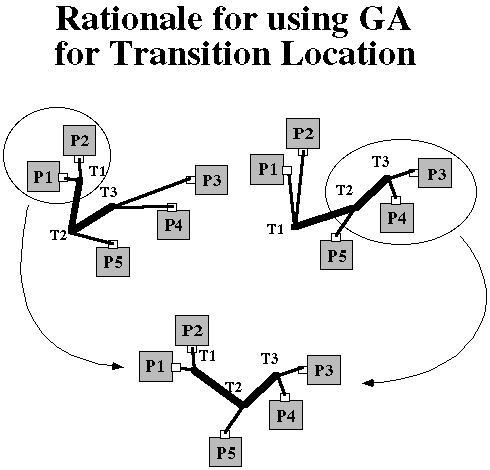
The Transition Locator has been formulated as a genetic problem to capitalize on the genetic algorithm(GA)'s ability to search large non-convex search spaces and on the inherent epistasis of the CHRP. The genetic approach is even more applicable here due to the nature of the transition location problem. As alluded to earlier, the GA takes a population of designs, in this case, different routings of a given configuration, and applies a combination of mutator and combinors to create the next generation. The GA, therefore, is able to combine parts of two different routings to create a new routing which is better than its parents. The figure below shows an example of two parents which if they exchange the location of transition T1, produce an offspring which has a lower cost than either parent.
Configuration Problem
Combinors fit the configuration problem well since it is able to use parts of configurations with high fitness. Consider the following example of two 7-transitioned cable harnesses. While each of them produce suboptimal routings, they both have parts which match the geometry well (shown with solid lines). If they are able to exchange fragments, then the offspring produced contains the qualities of both of the parents.

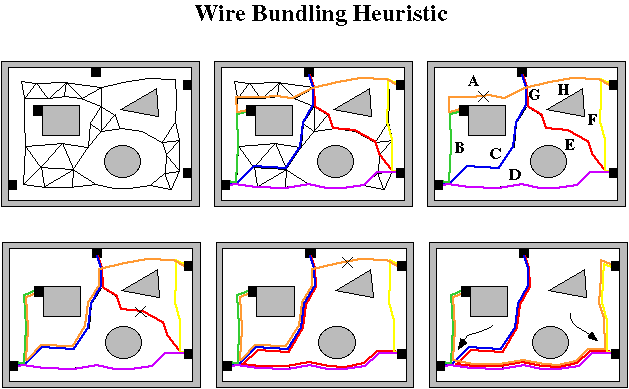
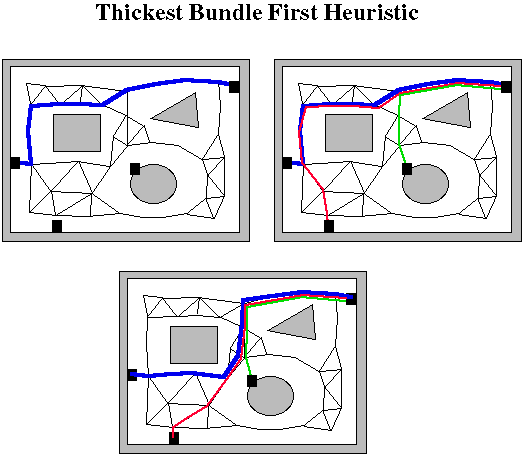
Several heuristic methods are used as creators. The Thick Bundle First agent, similar to Takashshi and Matsuyama's technique for the Steiner minimum spanning tree problem, builds the topology and routing simultaneously and incrementally. It starts by searching the wire list to find what pair of ports have the most wires in common. This is called the thickest bundle.
The shortest path between these ports is then routed. Next, the ports are sorted in non-increasing order by the number of wires emanating from them. A path is then routed from the ports to any node in the graph that is part of the routing in progress. These steps can be seen in the figure below
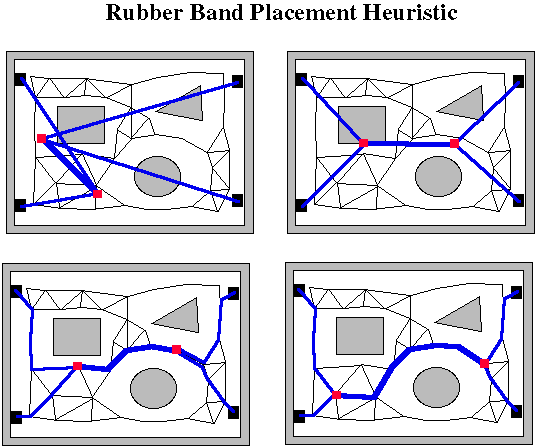
Another heuristic method, the rubberband router[conru 93], requires a topology as input and is useful in determining a quick routing for the topology. Routing is performed in three stages. First the transitions are placed in the environment using real coordinates instead of graph node location and are moved locally until a cost function is minimized
The Wire Bundling heuristic router is able to generate both a topology and a routing. It starts by finding the shortest path routing for each wire in the harness over the environment graph. The resulting routing, albeit not necessarily a cable harness itself, can be used as a lower bound estimate of the globally optimal harness routing. That is, since each wire is of shortest length, the total length of all the wires is minimized. Next, all of the links in the graph that are not used are removed leaving only links with one or more wires as shown below.